تدریس خصوصی و یادگیری ریاضیات
تدریس خصوصی و یادگیری ریاضیاتتدریس خصوصی و یادگیری ریاضیات
تدریس خصوصی و یادگیری ریاضیاتدرباره من
نظرسنجی
نظرسنجی
روزانهها
همه- بهترین و سریع ترین هاستینگ ایران با امکانات ویژه نت افزار بهترین و سریع ترین هاستینگ ایران با امکانات ویژه نت افزار نمایندگی هاستینگ سرورهای قوی سرویسهای طلایی و نقره ای با قیمت مناسب
- هاست و دامنه با قیمت فوق العاده و تخفیف باور نکردنی هاست ایران بهترین وب هاستینگ نمایندگی و ثبت دامنه
- ویدئوی آموزش ریاضی پایه حجم 194 مگابایت رمز فایل :www.p30day.com
- روشهای یادگیری ریاضی
- تدریس حرفه ای ریاضیات / تخفیف ویژه مخصوص رفع اشکال تدریس حرفه ای ریاضیات / تخفیف ویژه مخصوص رفع اشکال
پیوندها
دستهها
ابر برجسب
استرس امتحان تدریس خصوصی ریاضی در مشهد ریاضیات اضطراب ریاضی معادلات یادگیری ریاضیات تدریس حرفه ای انتگرال امتحان روش یادگیری اعداد آموزش ریاضی بخش پذیری ها تدریس ریاضیات تدریس خصوصی ریاضیجدیدترین یادداشتها
همه- تدریس خصوصی ریاضی و رفع اشکال
- با این 7 تیر به استرس امتحان شلیک کنید!
- اصول یادگیری بهتر ریاضی و دروس حل کردنی و مفهومی
- روز معلم مبارک
- شب یلدا مبارک
- تاریخچه عدد صفر
- عددی که بر 2 تا 10 بخش پذیر است
- عشق از نگاه ریاضی ( شعری از پروفسور هشترودی)
- روش یادگیری ریاضیات و سایر دروس یک بار برای همیشه
- برگه ریاضی مجتبی
- روشهای حل مساله
- نکاتی درباره بخش پذیری ها
- نوشته ای برای آنان که خواندن را دوست دارند - پرویز شهریاری
- تدریس خصوصی ریاضی در مشهد
- اضطراب ریاضی ( ترس از ریاضی)
بایگانی
- دی 1395 1
- دی 1393 1
- آذر 1393 1
- اردیبهشت 1393 1
- آذر 1392 1
- مهر 1392 2
- شهریور 1392 4
- خرداد 1392 2
- اردیبهشت 1392 3
- فروردین 1392 3
تقویم
دی 1395| ش | ی | د | س | چ | پ | ج |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
جستجو
روشهای حل مساله
1) جستجو برای الگو:
همواره کار حل مساله را با
نوعی ادراک شهودی از مساله شروع می کنیم و با بررسی چند حالت خاص به سوی
الگوسازی برای حل کامل آن جلو می رویم.
۲) رسم شکل:
در هر مساله ای
که امکانپذیر باشد رسم یک شکل (اعم از هندسی یا یک نمودار و غیره) می تواند
در یافتن حل مساله الهام بخش باشد و رابطه بین اجزا مساله را بهتر نمایان
می سازد.
۳) صورتبندی مساله معادل:
در بخش قبل دیدیم که گام نخست در
حل مساله عبارت است از جمع آوری داده - جستجو - فهمیدن مساله - برقراری
ارتباط بین اجزا - حدس زدن و تجزیه تحلیل. ولی اگر همه این کارها به روش
معقولی میسر نباشد چه کنیم؟ یعنی اینکه ممکن است کارهای محاسباتی خیلی
پیچیده باشد و یا به سادگی نتوانیم حالتهای خاصی را مطرح کنیم تا به بینش
لازم برسیم.آنچه در چنین شرایطی توصیه می شود این است که مساله را با مساله
ای معادل ولی ساده تر جایگزین کنیم. راه کلی در این گونه معادل سازی به
بینش و تجربه های عمومی باز می گردد ولی کارهایی از قبیل دستکاریهای جبری
یا مثلثاتی و تفسیر مجدد مساله با زبانی دیگر می تواند موثر باشد.
نکاتی درباره بخش پذیری ها
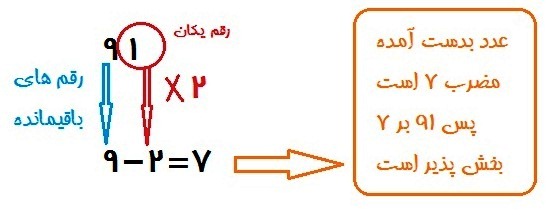
اگر یک عدد دو یا چند رقمی داشتیم برای بخش پذیری بر 7 ،
اول : رقم یکان را جداگانه در 2 ضرب می کنیم .
دوم : رقم های باقی مانده از همان عدد چند رقمی ( منظور به جز رقم یکان) را در نظر گرفته و از مقدار دو برابر رقم یکان ( قسمت قبل)کم می کنیم
سوم : اگر حاصل صفر شود یا عددی مضرب 7 بدست آید آن عدد بر 7 بخش پذیر است .
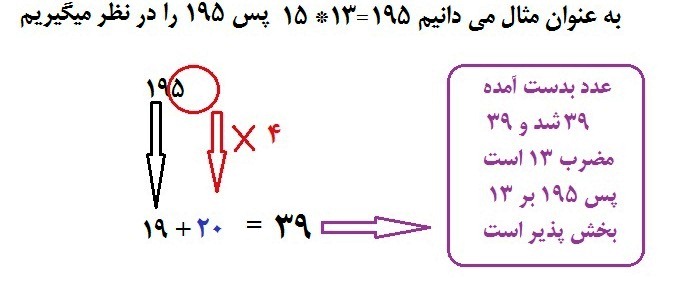
بخش پذیری بر 13 :
اول : رقم یکان را در نظر گرفته و آنرا 4 برابر می کنیم .
دوم : ارقام باقی ماندهاز آن عدد را با حاصل قسمت اول جمع می بندیم
سوم : اگر حاصل عددی مضرب 13 بدست آید آن عدد بر 13بخش پذیر است .
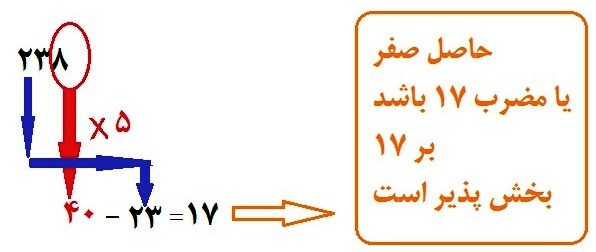
بخش پذیری بر 17:
اول : رقم یکان را در نظر گرفته و آنرا 5 برابر می کنیم .
دوم : سپس ارقام باقی مانده را از حاصل مرحله اول کم می کنیم
سوم : اگر حاصل صفر یا مضرب 17 باشد بر 17 بخش پذیر است
مثال : (می دانیم 238= 17*14 ) 238 را امتحان می کنیم داریم :
نوشته ای برای آنان که خواندن را دوست دارند - پرویز شهریاری
مقاله ای درباره آموزش ریاضی از پرویز شهریارینوشته ای برای آنان که خواندن را دوست دارند
پرویز شهریاری
بشر برای این نیامده که کورکورانه و از روی نادانی کار کند، بلکه
باید پیوسته با آنچه نادرست است در جدال و با آنچه نارواست در
جنگ باشد.
ژوزف ارنست رنان
روش آموزش امروزی، دو جنبه و یک هدف دارد. دو جنبه آن عبارت است از :
1- روش یادگیری
2- روش ارزیابی
هدف آن، تربیت آدم هایی است که بتوانند دشواری های جامعه خود یا جامعه جهانی را حل کند.
درباره روش یاد دادن سخنی نمی گویم، چون همه از آن آگاهیم و با آن بزرگ شده ایم و از نتیجه کم و بیش ناگوار آن هم، اطلاع داریم.
روش ارزیابی و نحوه امتحان را هم می شناسیم. تمام شرط ها را برای ترس و نگرانی دانش آموز فراهم می-کنیم و بعد در یک جلسه کوتاه، زیر فشار روحی بی اندازه ای، (دانش) او را (ارزیابی) می کنیم.
من به نادرستی این روش، که به نظرم از بیخ و بن نادرست است، نمی پردازم و تنها به چند نکته جانبی آن اشاره میکنم.
ادامه مطلب ...